Competition-Aware Lock Scheduling Algorithm in Transactional Systems

01 Background

Locks are the most commonly used mechanism to ensure consistency when multiple transactions (or applications) concurrently access a set of shared objects.

In a locking system, there are primarily two types of locks (intention locks also exist in database systems): shared locks and exclusive locks. Before a transaction can read an object (such as a tuple), it must first acquire a shared lock (also known as a read lock) on that object, essentially locking it. Similarly, before a transaction can request to write to or update an object, it must acquire an exclusive lock (also known as a write lock) on that object. As long as there are no exclusive locks on the object, the system can grant requests for shared locks. However, requests for exclusive locks on an object can only be fulfilled if no other locks exist on that object. When a transaction cannot immediately acquire the locks on the accessed object, it enters a blocked state until the rules mentioned above are satisfied. The system then awakens the transaction and grants it the corresponding locks.

This leads to a fundamental question: when multiple transactions compete for locks on the same object, which transaction should have priority to obtain the lock once it becomes available? This question constitutes the essence of lock scheduling. Despite the extensive focus on concurrency control and locking protocols, surprisingly, very little attention has been paid to lock scheduling. Furthermore, while there is a substantial body of research on scheduling in real-time systems, these efforts make a shared assumption that when load requests arrive in the system, their execution times are either known or have explicit execution time limits.

The following characteristics of lock scheduling render it a uniquely challenging issue, particularly when considering the performance of real-world database systems.

• Online nature: When a transaction is granted a lock, the system doesn't know when that transaction will release the lock. The execution time of a transaction is only known once the transaction concludes.
• Intricate dependencies: Dependencies exist within the DBMS. When a transaction is awaiting a lock held by another concurrent transaction, a dependency is formed. In practice, these dependencies can be quite complex, as each transaction can hold locks on multiple objects, and multiple transactions can hold shared locks on the same object.
• Inconsistent access patterns: Objects in the database do not have equal popularity. Furthermore, different transactions have varying access patterns.
• Multiple lock modes: Granting exclusive locks to write transactions or shared locks to multiple read transactions is the root of the problem's complexity.

Addressing these characteristics, the paper elaborates on the proposed competition-aware lock scheduling algorithm.

The paper stipulates that the system adheres to the Strict Two-Phase Locking (Strict 2PL) protocol: once the system grants a transaction the corresponding lock, it holds onto that lock until the transaction's conclusion. Once a transaction completes execution (either by committing or being aborted), it releases all the locks it held.

02 Problem Modeling and Lock Scheduling Algorithm

The lock scheduling problem revolves around determining which transaction acquires a lock under the occurrence of the following two events:

1. When a transaction requests a lock,
2. When a transaction holding a lock releases it.

Given a set of transactions T and the entirety of database objects O within the system at a specific moment, the paper defines the system dependency graph as a graph G = (V, E, L) with edge label information. Here, the graph's vertices V constitute the set T∪O, representing both transactions and database objects. The edges E are defined as: E⊆T × O∪O × T, depicting the locking relationships between transactions and objects. Specifically, for a transaction t ⊆ T and an object o ⊆ O,

• (t, o) ϵ E if transaction t is waiting for a lock on object o,
• (o, t) ϵ E if transaction t holds a lock on object o.

The edge labels L: E→{S, X} denote the type of lock:

• L(t, o) = X implies that transaction t is waiting for an exclusive lock on object o,
• L(t, o) = S implies that transaction t is waiting for a shared lock on object o,
• L(o, t) = X indicates that transaction t holds an exclusive lock on object o,
• L(o, t) = S indicates that transaction t holds a shared lock on object o.

Ensured by the deadlock detection module, graph G forms a Directed Acyclic Graph (DAG).

Assuming G is the collection of all such DAGs within the system, the lock scheduling problem can be reduced to a pair of functions corresponding to the two aforementioned events, denoted as A = (Areq, Arel): Ⓖ × O × T × {S, X} → 2^T. For instance, given the system dependency graph G, when transaction t requests an exclusive lock on object o, Areq(G, o, t, X) determines which transaction currently awaiting lock requests on o (including t itself) should be scheduled.

Likewise, with the graph G, when transaction t releases a shared lock on object o, Arel(G, o, t, S) determines which transactions currently waiting for lock requests on o (including t itself) should be scheduled. Note that, according to the previously defined DAG, apart from transactions themselves, the lock types requested and the intensity of lock contention are also captured within G. Based on this, the paper defines a category of competition-aware lock scheduling algorithms that determine transaction priorities based on their impact on overall system competition.

The paper delves into several mechanisms to implement competition-aware lock scheduling algorithms. The first approach is to infer that a transaction that holds more locks is more likely to obstruct other transactions, thereby having a higher priority (Most Lock First, MLF).

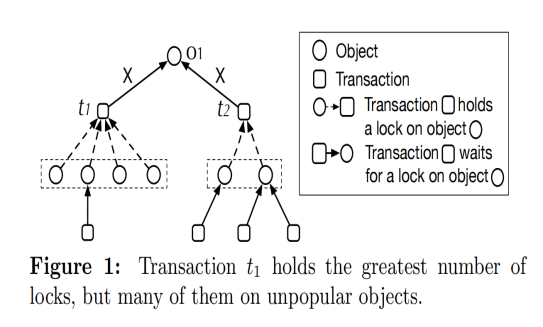
As illustrated in Figure 1, transaction t1 holds a higher priority compared to transaction t2, with the former holding 4 locks while the latter holds only 2 locks. However, this approach overlooks the issue of hotspots—transactions may hold a significant number of locks on cold data, which doesn't substantially impact system operations. An informed strategy is to consider only locks that are awaited by transactions (Most Blocking Lock First, MBLF).

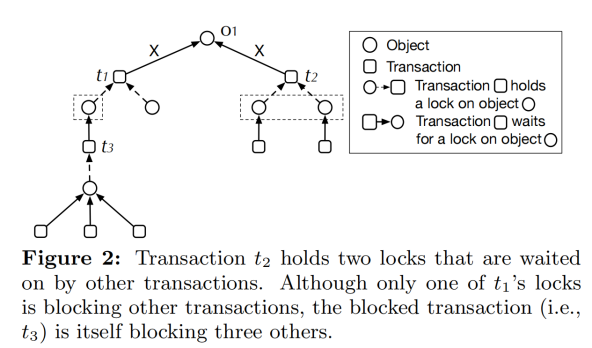
According to this criterion, transaction t2 in Figure 1 holds a higher priority than transaction t1, as t2 possesses two awaited locks, whereas t1 has just one. However, this method also has limitations—it treats locks with multiple competing transactions as if there's only one waiting transaction for each lock. Figure 2 showcases the shortcomings of this approach.

Following the MBLF criterion, transaction t2—blocking the execution of two transactions—should be scheduled before t1. While t1 has just one waiting transaction (t3), t3 itself blocks the execution of three other transactions. Choosing to run t2 first based on MBLF could potentially prolong system-blocking times.

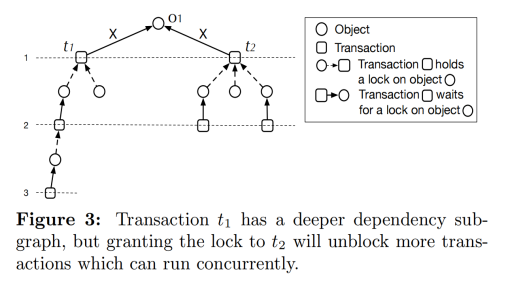
A more intricate strategy involves considering the depth of transaction dependency subgraphs, termed Deepest Dependency First (DDF). The rationale here is that subgraphs with longer paths could potentially obstruct more transactions. As depicted in Figure 3, transaction t1's subgraph depth is 3, whereas t2's is 2. Consequently, t1 enjoys higher priority.

However, this method is flawed as it solely addresses hotspot locks from a depth perspective, lacking a comprehensive view of overall system operations. Considering the limitations of the above algorithms, the paper introduces the Largest Dependency Set First (LDSF) algorithm, which offers formal guarantees for expected average latency.

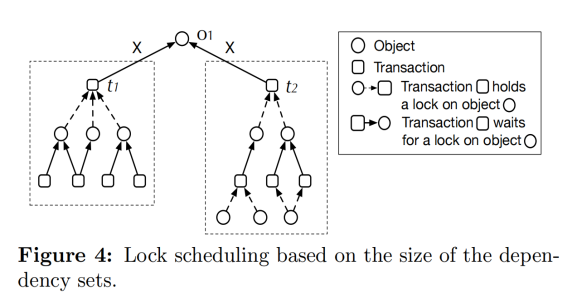
Given two transactions t1 and t2 within the system, if a path exists from t1 to t2 in the directed acyclic graph, t1 is considered dependent on t2. The dependency set g(t) of transaction t comprises all transactions dependent on t. The LDSF algorithm employs the size of different transaction dependency sets to determine the priority of which transaction(s) to schedule. For example, in Figure 4, transaction t1's (including itself) dependency set size is 5, while transaction t2's is 4.

Thus, if both t1 and t2 request an exclusive lock on object o1, LDSF would prioritize granting the lock to t1 (over t2).

LDFS treats all transactions requesting shared locks on object o as a single transaction. Therefore, the dependency set of transactions requesting shared locks on object o is the union of the dependency sets of all transactions requesting shared locks on that object. For transactions requesting exclusive locks, the algorithm selects the one with the largest dependency set and compares it with the dependency sets of transactions requesting shared locks, selecting the one with the larger dependency set for execution.

If shared locks are to be granted, all transactions awaiting shared locks acquire the lock. In a scenario where only exclusive locks are present, LDSF is the optimal algorithm in terms of expected average latency. The intuitive reasoning behind this is that if transaction t1 is dependent on t2, any progress made by t2 can also be considered progress for t1 since t1 cannot obtain its requested lock until t2 completes.

Hence, by granting locks to transactions with the largest dependency sets, LDSF allows the maximum number of transactions to make progress until completion.

However, in cases involving shared locks, the above scenario doesn't always hold true. Even if transaction t1 depends on t2, the execution of t2 doesn't necessarily affect the progress of t1. For instance, as illustrated in Figure 5, while t1 relies on t2 and t3, the execution of t2 may not impact t1's progress unless concurrent transaction t3 releases its held shared lock before t2.

As previously stated, LDSF grants shared locks to all transactions awaiting the lock. However, this isn't an optimal strategy. Generally, granting numerous shared locks on the same object increases the likelihood of long transactions. Until a long transaction releases its locks, no exclusive locks can be granted on that object. In other words, the expected duration of holding shared locks increases with the number of transactions, a phenomenon known as the "straggler" problem, exacerbated with increasing concurrent processes/threads. Given that granting shared locks to more transactions might delay exclusive lock requests, it's easy to consider that exclusively granting shared locks to a subset of waiting transactions might reduce the overall system latency.

Based on these considerations, the paper introduces a batched LDSF (bLDSF) algorithm, which only grants shared locks to a subset of shared lock requests on object o. It introduces a delay factor f(k), representing the ratio of the speed of granting locks to k transactions together (using the maximum remaining time of the k transactions as a random variable representing the mathematical expectation) compared to granting locks to each transaction individually (using the random variable of the remaining time of the running transactions in the system as a random variable representing the mathematical expectation). f(k) quantifies how much longer it takes, on average, to release shared locks held by a batch of k transactions compared to a single transaction.

The delay factor f(k) on random variables representing the remaining execution time of independent and identically distributed transactions satisfies the following conditions:

1. f(1) = 1
2. f(m) < f(m + 1), strictly monotonically increasing
3. f(m) ≤ m, sublinear function

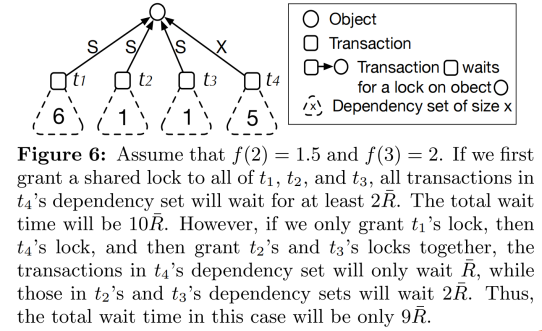
Figure 6 provides an illustration of the bLDSF algorithm. Assuming f(2) = 1.5 and f(3) = 2, if shared locks are granted in a batch to transactions t1, t2, and t3, then t4's wait time is 2R (where R represents the average delay of transaction runtime), resulting in a total wait time for transaction t4's dependency set of 10R (5 × 2R). If the lock-granting order is t1, t4, (t2, t3), the total wait time becomes 5R + 2 * 2R.

Unlike the LDSF algorithm, bLDSF necessitates the analysis of the delay factor. However, since the remaining runtime of transactions can be modeled as random variables, the exact functional form of delay factor f(k) will also depend on the distribution of these random variables.

03 Implementation and Experiments

Starting from MySQL 8.0.3, the default lock scheduling algorithm has been switched to bLDSF. Specifically, all pending lock requests on an object are placed in a queue. Lock requests are granted to arriving transactions immediately only if either of the following conditions is met:

Both conditions must be satisfied:

1. There are currently no other locks held on the object.
2. The requested lock type is compatible with all current locks on the object, and no incompatible requests are ahead in the waiting queue.

Similarly, whenever locks on an object are released, MySQL's lock manager scans through the entire queue. It schedules transactions for any lock request as long as the above conditions hold true. Once the scheduler encounters the first lock request that can't be granted, it stops scanning the rest of the queue. One of the challenges in implementing LDSF and bLDSF is tracking the size of transaction dependency sets.

In practical implementation, the exact value of transaction dependency set size is not required; an approximate value suffices. |g(t)| = ∑|g(t′)| + 1, where t′ is a transaction in the dependency set of t. Another challenge in implementation lies in finding a batch of transactions that fulfill the requirements for bLDSF. The algorithm first sorts transactions by their dependency set sizes in descending order, then iterates over k = 1, 2, 3, ... to find the maximum value of |g(t)|/f(k). Afterward, it determines the type of lock to schedule. The experiments compared the aforementioned heuristic algorithms, FIFO, and the VAST algorithm (Variance-Aware Transaction Scheduling, which prioritizes the transaction with the longest waiting time when multiple transactions are waiting to acquire the same lock on a data object, rather than a simple first-come-first-served approach). The experiments were conducted on an environment with an Intel(R) Xeon(R) E5-2450 16-core CPU and a 5GB cache configuration. The test dataset included TPCC and custom microbenchmarks. Here are several test results (detailed results are available in the paper).

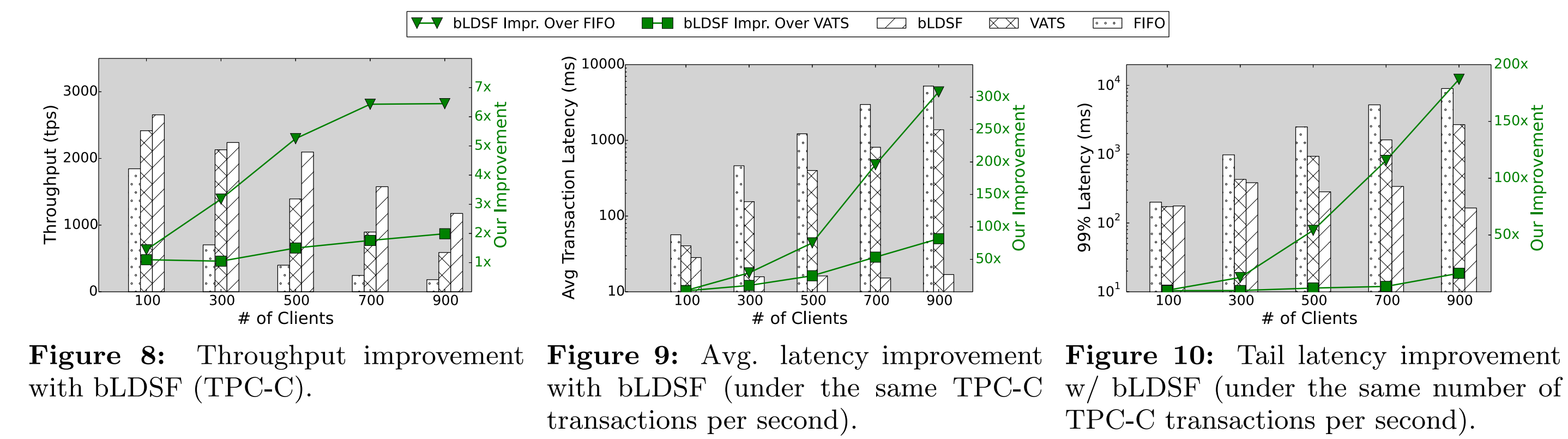
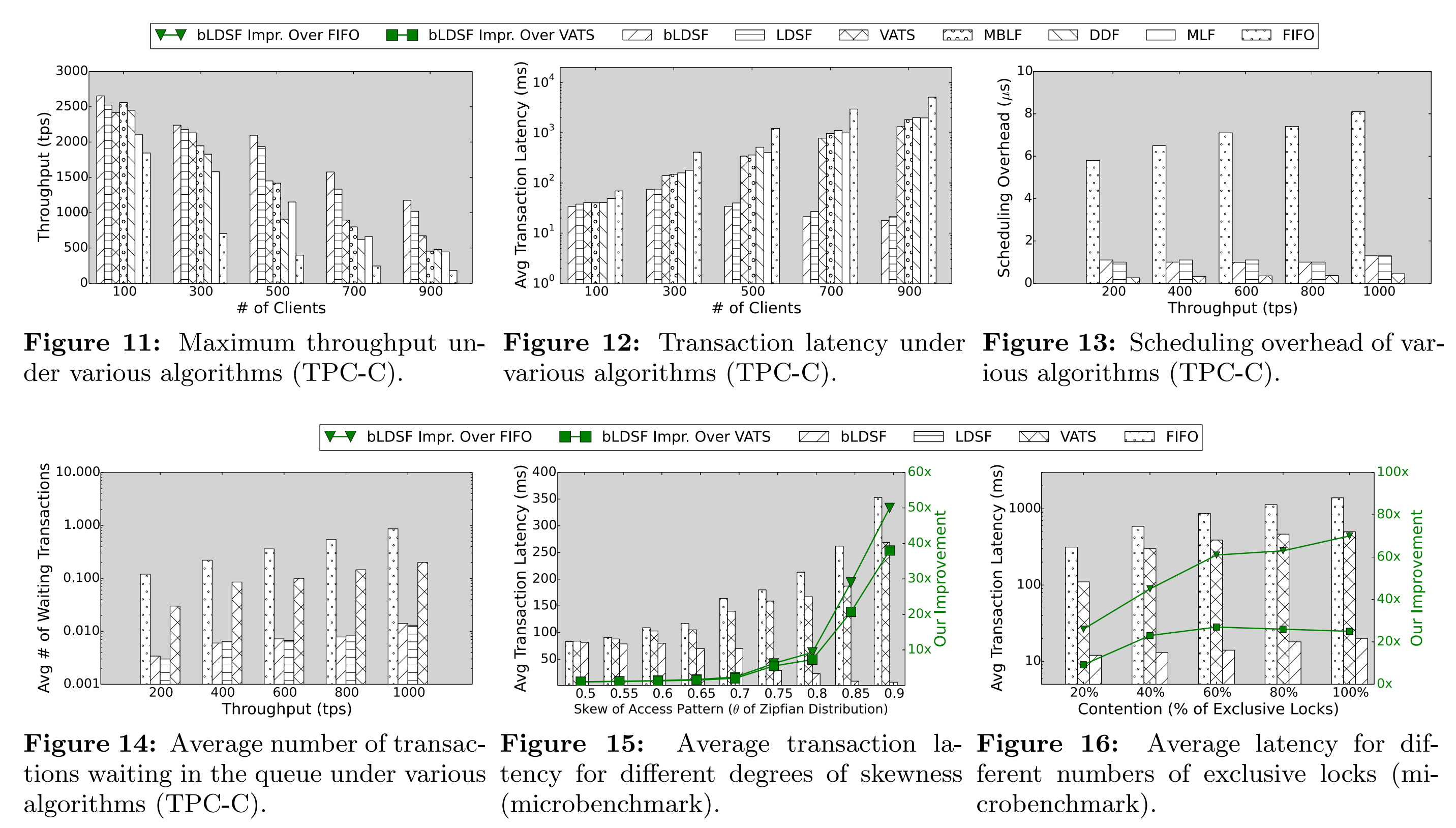
In terms of throughput, with 100 connections, bLDSF outperforms FIFO by 1.4 times and VATS by 1.1 times. However, with 900 client connections, bLDSF achieves a throughput 6.5 times higher than FIFO and 2 times higher than VATS. As shown in Figure 9, the bLDSF algorithm significantly outperforms FIFO by 300 times and VATS by 80 times. The paper also reports P99 latency in Figure 10. bLDSF's performance is 190 times higher than FIFO. Interestingly, bLDSF's performance is also better than VATS (up to 16 times), even though VATS is designed specifically to reduce tail latency. This is because, on average, the bLDSF algorithm allows transactions to complete faster, reducing the waiting time for transactions at the end of the queue and resulting in lower tail latency. The paper also provides comparisons of other heuristic algorithms in terms of factors like throughput and latency, as shown in Figures 11 to 16.

04 Conclusion

In the era of multi-core processors, research in the database systems community has primarily focused on reducing competition for critical section resources within lock managers.

In general, there are three main approaches:

1. Reducing the frequency of acquiring locks.
2. Alleviating the exclusiveness of atomic operations during lock acquisition.
3. Further parallelizing the lock manager to mitigate competition for lock resources.

For instance, the lock inheritance technique adopted by PostgreSQL falls into the first category. Contention-aware locking technology takes a global perspective, aiming to advance transactions running within the system as quickly as possible. It possesses both strong theoretical foundations and practical applicability.

This algorithm is currently the default lock scheduling algorithm in MySQL 8.0.3 and beyond. Interested readers can delve into the code implementation. Finally, as a thought-provoking question, why didn't the paper consider intent locks? Welcome everyone to explore and discuss this topic together.

END

Image Source：

Paper: Contention-Aware Lock Scheduling for Transactional Databases